第二节 评估与预测方法
一、危险物品安全性评估方法
(一)安全性评估方法概述
安全评估分狭义和广义二种。狭义指对一个具有特定功能的工作系统中固有的或潜在的危险及其严重程度所进行的分析与评估,并以既定指数、等级或概率值作出定量的表示,最后根据定量值的大小决定采取预防或防护对策。广义指利用系统工程原理和方法对拟建或已有工程、系统可能存在的危险性及其可能产生的后果进行综合评价和预测,并根据可能导致的事故风险的大小,提出相应的安全对策措施,以达到工程、系统安全的过程。本书以危险物品为讨论对象,所涉及的安全评估是狭义的安全评估,它又称风险评估、危险评估,或称安全评价、风险评价和危险评价。
对于一个项目或指定目标的安全评估,包括:管理制度的评估、物理安全的评估、化学安全的评估、生物安全的评估、计算机系统安全评估、网络与通信安全的评估、日志与统计安全的评估、社会秩序安全的评估、安全保障措施的评估、总体评估等方面的内容。在危险物品管理领域,涉及人与财务的安全评估、管理制度的评估、安全保障措施的评估三方面内容。
安全评估的方法一般是指标体系评分法,首先需要针对指定的项目或内容,建立一套安全评估指标体系,即评估方案,指标体系分为一级指标、二级指标……,最后一级指标是得分点。然后对最后一级指标进行逐项打分,得分累加后形成上一级指标的分值,依次类推最后形成总分值。
各指标得分数值的确定常用德尔菲法或数理模型法。采用德尔菲法须有得分说明,采用数理模型法需要先建立模型,说明数值来源、形式等。
(二)德尔菲法
德尔菲是Delphi的中文译名。德尔菲法,也称专家调查法,1946 年由美国兰德公司创始实行,其本质上是一种反馈匿名函询法。该方法是由管理机构组成一个专门的评估机构,其中包括若干专家和评估对象相关单位或行业的管理者,按照规定的程序,背靠背地征询专家对评估项目的意见或者判断,得出结论或分值的方法。
该方法广泛地应用于商业、军事、教育、卫生保健等领域,在使用过程中显示了它的优越性和适用性,受到了越来越多研究者的青睐,应用领域逐渐拓宽,目前几乎所有领域都有应用。
1. 德尔菲法的工作流程
德尔菲法的一般流程是在对所要评估的项目征得专家的意见之后,进行整理、归纳、统计,再匿名反馈给各专家,再次征求意见,再集中,再反馈,直至得到基本一致的意见,流程图见图3-1。
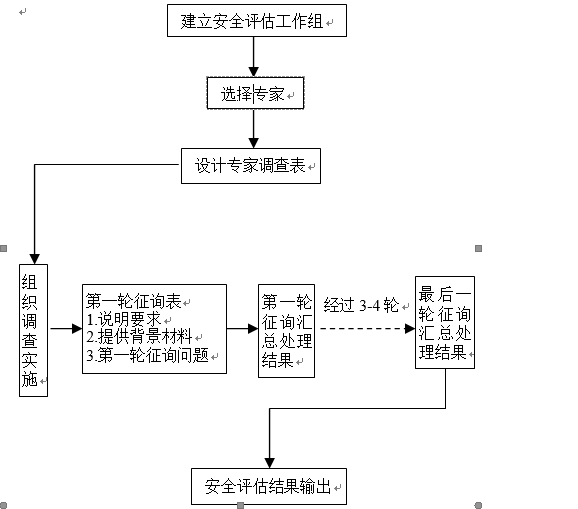
图3-1德菲尔法工作流程图
2. 指标权重的层次分析法确定
以炸药仓库风险评估为例,用层次分析法确定二级指标的权重。一级指标是“炸药仓库风险A”,二级指标分别是“爆炸风险B1”、“火灾风险B2”、“流失风险B3”、“失效风险B4”、“被盗风险B5”。 流失风险是指由于管理不善,造成炸药没有记录地消失的风险;失效风险是指水淹、水汽侵蚀、久置不用等因素造成炸药失去原有的爆炸性能的风险。
(1)A---B判断矩阵。根据层次分析模型,首先构造一级指标判断矩阵。
根据调研情况和对已掌握的案例分析的结果,5个二级指标与一级指标关系密切程度的排列顺序是B1≈B5 > B2≈B3>B4。
按照A.L.Saaty1-9标度法,根据贡献准则相对比较,建立相对重要性判断矩阵A-B如下:
 我们用方根法计算最大特征根。具体计算步骤如下:
我们用方根法计算最大特征根。具体计算步骤如下:
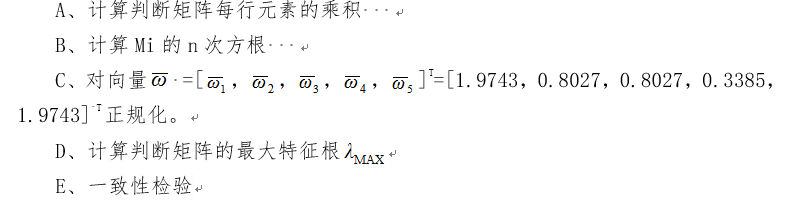
3. 专家数据的四分位法处理
给专家的征询表回收后,必须对专家繁杂多样的回答进行处理,才能获得有用的信息,才能成为下一轮征询题的内容,并促使专家意见收敛。对专家意见的处理通常不用平均数,因为平均数不能反映数据分布,而且个别过大或过小的数据会对平均数产生较大的影响。一般四分位数法处理。
如果专家做出的答案是量化的,如数据或时间答案,则可以使用四分位数法进行处理。四分位数(Quartile)是统计学中处理统计数据的方法,它把所有数值由小到大排列成序,并分成四等份,处于1/4、1/2、3/4分割点位置的数据就是四分位数。
第一四分位数 (Q1),又称“下四分位数”,是该样本中所有数值由小到大排列后第25%位的数字。
第二四分位数 (Q2),又称“中位数”,是该样本中所有数值由小到大排列后第50%位的数字。
第三四分位数 (Q3),又称“上四分位数”,是该样本中所有数值由小到大排列后第75%位的数字。
(Q3-Q1)称为四分位距(InterQuartile Range, IQR),反映50%专家风险评估值的分布范围。
用四分位数法处理数据时,先将回收的n个专家的答案从小到大排成顺序数列,即:x1≤x2≤...≤xk≤...≤xn-1≤xn,k为1至n之间的正整数。
例3.1 某市公安局风险评估2018年该市烟花爆竹相关事故的起数,20位专家返回了第一轮风险评估值。按从小到大顺序为:53.5, 58.0, 62.4,63.7, 67.5, 68.6, 71.3,72.6, 75.5, 78.5, 80.0, 81.4, 83.6, 84.8, 86.6, 88.5, 89.2, 90.0, 92.5, 95.7。请用四分位数法处理。
处理过程如下:
由于n = 20,是偶数,中位数Q2用(3-2)式计算。
因为k = n/2 = 20/2 = 10,Q2=(x10+x11)/2 =(78.5+80.0)/2 =79.25。
由于k = 10,是偶数,用(3-6)式计算Q3;用(3-10)式计算Q1。
Q3 =(x15+x16)/2=(86.6+88.5)=87.55。
Q1 =(x5+x6)/2=(67.5+68.6)/2 =68.05。
风险评估值的全距是所有数据中最大值与最小值之差 =95.7 - 53.5 =42.2
四分位距(Q3-Q1) =87.55 - 68.05 =19.5。
四分位距反映专家意见的集中情况,四分位距越小,专家意见越集中,反之,越分散。本例题中四分位距占风险评估值全距的46.2%,50%的征询专家的风险评估值间距小于全局的50%,说明数据相对集中,它是风险评估值收敛的前兆。如果四分位距占风险评估值全距的比例超过50%,很有可能在以后几轮的调查中会出现两极或多级分化的现象,应当尽早采取措施避免。
统计结果常用截角楔形图表示,顶点是中位值,两端是四分位值,相当于给出3个数据。坐标长度表示全程,楔形图框内表示四分位距。如图3-2所示。
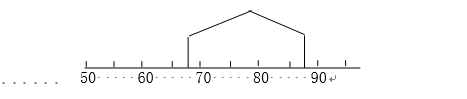
图3-2 四分位数截角楔形图
在下轮征询时,将统计结果反馈给专家组,让专家再思考自己上轮的风险评估。风险评估远离四分位区间的专家,会重新审视自己的风险评估过程,重新进行风险评估;四分位区间内的专家也会审视中位数的合理性,再度风险评估。如果下一轮四分位区间向中位数靠近,则风险评估过程收敛性良好。见图3-3。
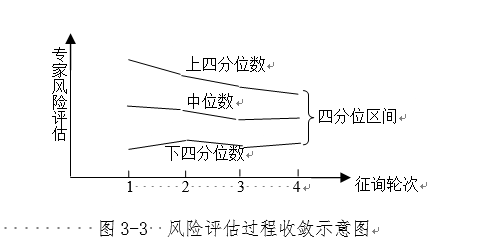
(二)专家意见的一致性判别
对某方案的风险评价,不仅需要知道各位专家对该方案j风险评价分值的高低,以确定方案的好坏,也需要知道专家对该方案j风险评价分值相近程度。评价分值越接近,说明专家对该方案风险的看法趋于一致,评价总体结果越可靠;若评价分值远离,说明存在的意见分歧较大,评价总体结果不可靠。体现专家意见一致性的处理方法,通常是方差分析方法,根据所用数据来源的不同,所形成的指标又分为变异系数和协调系数。
1. 变异系数
以专家的评价分值和评估等级为基础,针对个体方案,经方差分析得出的系数为变异系数。
(1)以评价分值为基础的变异系数。
(2)以评估等级为基础的变异系数。
2.协调系数
以专家的评估等级为基础,针对所有方案,辨别本轮调研专家组意见的一致程度,经方差分析得出的系数为协调系数。
协调系数W为:
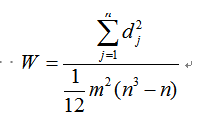
W在0-1之间,W越接近1,则专家意见一致性越好;反之,W越接近0,则专家意见分歧严重,需要分析原因。如果专家意见分歧严重的结果反馈给专家组后,收回的征询意见仍然存在较大的分歧,则可能是各流派的观点不能调和,需要采取一定措施解决。
如果组织者宣传、动员工作较为出色,所选征询专家认真负责,回收意见份数m(多数情况下就是专家数)等于每个方案得到的评价数目。对于个别专家漏填某个方案评价意见的情况,应尽量采用补救措施,形成完整的答卷。避免因每个方案的评价数目不同,对评价结果产生影响。也可采用网上填报的方式,存在漏填项目则无法提交,以保证提交答卷的完整。若出现了不完整的答卷,又无法弥补,这时的m应改为mj,mj是对方案j风险的评价数目。
方差分析不仅用于评分排队法,也可用于最终以数值形式体现专家意见的集中程度分析。
调查问卷的处理方法很多,适用于德尔斐法的方法也不少,但各种方法都有长处和弱点,有适合使用的条件。在方法选择时应充分考虑体现征询问题的特点,反映回收意见的主要特征,以及是否能对下一轮征询起到积极的作用。
(三)数理模型法
随着计算机的普及,大量计算变得十分便捷,这使得数据处理倾向于大型化和复杂化,数据与数学方法的应用受到重视,数理模型法孕育而生并得到广泛推广,在各行各业都有应用。数理模型法是运用数学符号和数字算式的推导来研究和表示研究对象变化过程和相关现象的研究方法。
前面所述的事件树分析定量计算枪弹库盗窃案件发生的概率;采用事故树分析法分析S区盗窃案件影响因素重要度的计算;采用灰色系统理论计算江苏刑事犯罪变化趋势等等都是运用数理模型法的典型案例。
指标分值的获取除了可以采用德尔菲法等方法之外,还可以采用数理模型法获取,仍以“炸药仓库风险A”为例,其“火灾风险B2”下可分为“自燃风险C1”、“电气火灾风险C2”、“烟头火灾风险C3”、“用火不慎火灾风险C4”、“雷击火灾风险C5”、“纵火火灾风险C6”、“小孩玩火火灾风险C7”、“静电点燃火灾风险C8”等。“自燃风险C1”可利用“弗兰克-卡门涅茨基模型”推算安全体积,结合风险评估项目中可燃物堆垛体积、平均存放时间,计算风险概率,形成该三级指标的得分。
二、事故预测一般方法
如果把评估作为一种宏观判别危险性的方法,则预测是微观判别方法。预测也分为定性与定量两类方法,由于定性预测是宏观描述,其精确性不及安全评估,它已被安全评估所替代,因而目前的预测一般都是定量预测。
定量预测需要基础条件,一是对事物发展变化规律有正确的认识,掌握了其变化规律,而且对这种变化规律的认识需要到达量化表述的程度,即存在数学计算式表达方式。二是计算数据来源所处的政治、经济、社会、气候、地理、人的安全状态、无得安全状况等环境应稳定,且与所需要预测目标所处的上述环境基本相同,数据形成环境的变化将在很大程度上影响预测的准确度。三是需要正确认识事物之间的联系。联系普遍存在,事物之间或各因素之间的相互影响不能忽视。因此,预测常常需要建立一个相对独立系统,这个系统与外部事物的相互影响较小,但系统内部各部分、各组件、各环节、各因素之间的联系往往较为紧密,需要统筹考虑。四是实事求是,以客观事物、客观数据、客观现象为基础,不参杂主观因素。对于一时不能量化的客观现象,不能主观臆断。五是需要大量观察,获取大量数据,达到量化计算所需的最低样本量。样本覆盖面应该广泛、全面,反映出该事物的各个方面的性质、特征。现象反映本质,单一现象反映一项本质,但一项本质可以反映出一类多个现象,不能以现象描述的数量确定是否全面描述事物的本质,而应该从不同角度、不同类别描述事物,反映出其本质。
基于上述限制因素,定量预测的条件要求较高,适用面收到限制,正是这一原因,定量预测的应用范围不及安全评估宽泛。
单一变量的预测计算方法很多,多数现有的物理学计算公式都是事物内在规律的描述,都可以变成定量预测的计算模型,但是,客观事物的影响因子很多,变量很多,在大数据云服务应用之前,多为单一变量模型预测。单一变量模型预测只能以主要因素为变量,忽视次要因素的影响,使得预测准确度差,应用受到限制。与危险物品管理相关的模型预测方法除了事件树分析、灰色系统理论分析等方法外,还有:
1. 回归分析预测法。回归分析方法预测犯罪是最早运用于犯罪预测的数理方法,它利用数理统计原理,对大量的统计数据进行数学处理,确认因变量与自变量之间的关系,建立一个相关性显著的回归方程,并加以外推,用于预测未来因变量数值变化的分析方法。他可以分析某类事故或案件变化趋势,也可分析某种因素导致事故或案件变化趋势。
2. 圆周假设预测盗窃犯住地。坎特等人通过研究发现,犯罪人对犯罪地点的选择有限,他们又受地理环境的熟悉程度、时间、受害人工作性质、机会、犯罪成本、危险性、舒适程度、信心和获利寡众等多种因素的限制。坎特等人提出了犯罪人住地的圆周假设(circlhypothesis):将犯罪全部标注在地图上,假定具有某特征的假冒伪劣烟花爆竹销售是由一个人所为。以两个最远的销售地点之间的距离为直径,可以画一个包括所有销售地点的圆周,则这个销售者极有可能住在这个圆周内,并且很可能就住在靠近圆形中心的某个地方。
3. 最优组合预测法。实际的预测对象通常是较为复杂的社会经济系统,有多种错综复杂的因素对其产生影响。单项预测方法抛弃误差较大的模型方法,选择一个最好的模型方法。但不同模型方法有各自的优点和缺点,它们并不相互排斥,而是相互联系、相互补充。若把多种单项预测方法正确地组合起来,则能提高预测的精确度和可靠度。组合预测就是设法把不同的预测模型组合起来,综合利用各种预测方法所提供的信息,以适当的加权平均形式得出组合预测模型。组合预测最关键的问题就是求出加权平均系数,使得组合预测模型更加有效地提高预测精度。
三、大数据预测事故/案件方法简介【知识拓展】
预测必须考虑各种因素对预测项目的影响,还需考虑各种因素之间的相互作用,这很像神经网络的工作模式。人工神经网络是由大量简单的高度互连的“神经元”所组成的复杂网络计算系统。神经网络预测控制属于智能型预测控制的范畴,它将神经网络技术与预测控制相结合,弥补了传统预测控制算法精度不高、仅适用于线性系统、缺乏自学习和自组织功能、鲁棒性不强的缺陷。它可以处理非线性、多目标、约束条件等异常情况,它具有函数逼近能力、自学习能力、复杂分类功能、联想记忆功能、快速优化计算能力,以及高度并行分布信息存贮方式带来的强鲁棒性和容错性等优点。
从理论上讲,大数据预测事故/案件是先兆识别理论的应用,事故与违法犯罪都有先兆,大数据挖掘是从大量数据中寻找规律,预测未来发生的事件。为了数据分析,需要收集指定防护目标的所有数据,包括人的行为数据和物的安全数据,甚至包括看似无关紧要的数据,为此需要建立或完善现有的公安数据库,创建人和物行为轨迹数据库,创建危险物品标识制度以及从生产到消亡全流程的数据库等等。只有建立了精确完善的数据库体系,大数据预测才能准确。
2011年,美国加利福尼亚州圣克鲁兹的警察局测试了一种名为“PredPol”的犯罪预测软件。过去6个月,洛杉矶警察局也对这款软件进行了测试。两地警察局的测试结果均显示PredPol拥有不俗的预测能力,犯罪率大幅降低。在洛杉矶,软件实施地区的盗窃行为减少了33%,暴力犯罪减少了21%。该软件正在美国150多个城市试用,并将逐步在美国全境内推广。我国大陆2013年出现首本全面阐述犯罪预测的专著,2015年江苏苏州开始研究和试运行。由于数据缺乏,预测准确度有待于提高。
